Basis For Column Space

Since the column space of a consists precisely of those vectors b such that a x b is a solvable system one way to determine a basis for cs a would be to first find the space of all vectors b such that a x b is consistent then constructing a basis for this space.

Basis for column space. The column space of an m n matrix with components from f displaystyle mathbb f is a linear subspace of the m space f m displaystyle mathbb f m. The dimension of the column space is called the rank of the matrix and is at most min. For each of column vectors of a that are not a basis vector you found express it as a linear combination of basis vectors.

It s a property that it possesses. Find a basis for the nullspace row space and the range of a respectively. Now we show how to find bases for the column space of a matrix and the null space of a matrix.

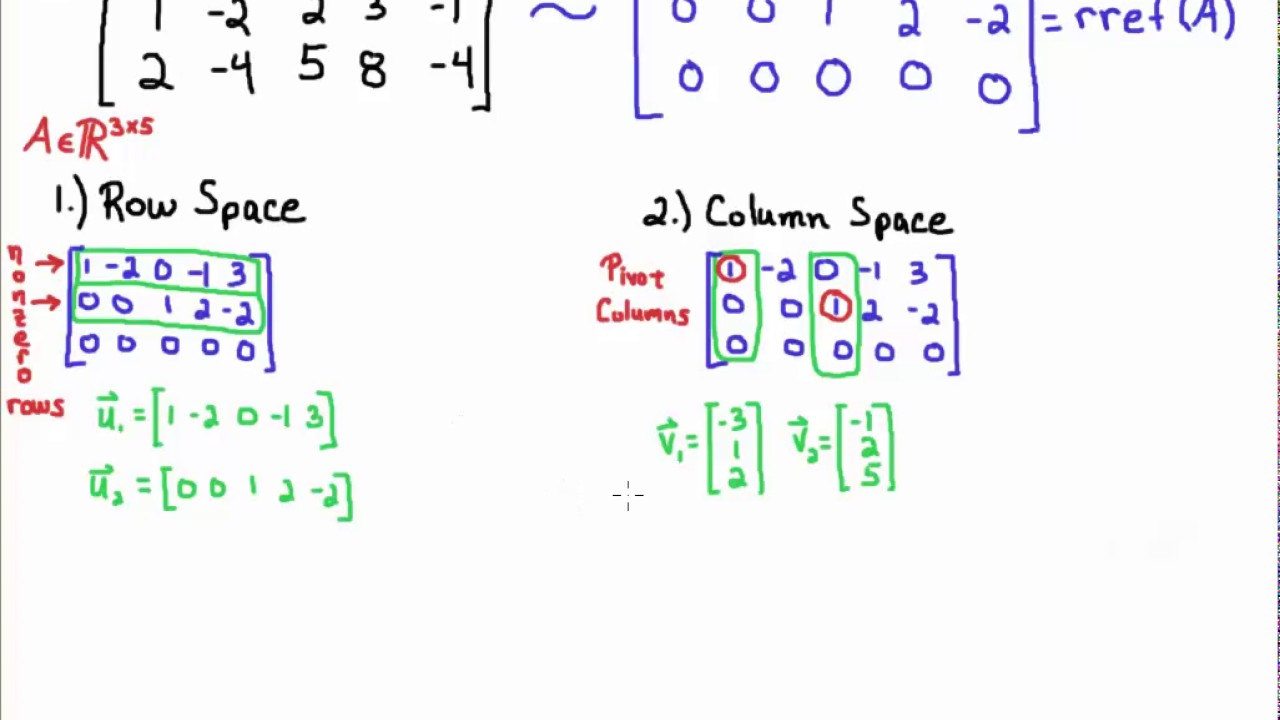
See this important note in section 2 6. Thus basis for col a r 2 r 1 r 2 r 3 2r 1 r 3. The subspace of rm spanned by the column vectors of a is called the column space of a.

The subspace of rn spanned by the row vectors of a is called the row space of a. Calculate a basis for the column space of a matrix step 1. Null space calculator.

The column space of a matrix is the image or range of the corresponding matrix transformation. We now turn to the main de nitions of this section. The column space calculator will find a basis for the column space of a matrix for you and show all steps in the process along the way.

De nition 357 let a be an m n matrix. Let f displaystyle mathbb f be a field. In order to find a basis for a given subspace it is usually best to rewrite the subspace as a column space or a null space first.