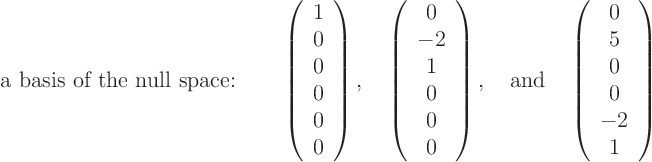Basis For Null Space

B let b v 1 v n 1 be a basis of the row equivalent matrix bases for the null space range and row space of a matrix let.

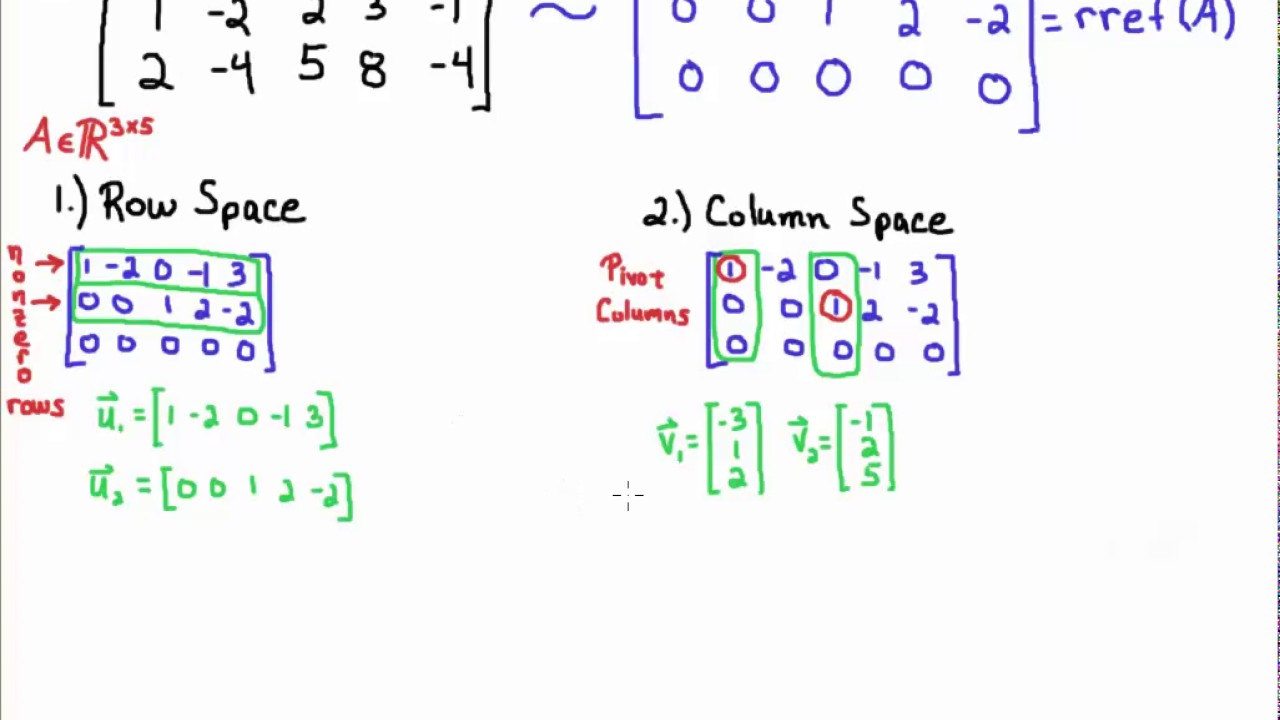
Basis for null space. So the null space is the set of all of vectors in r4 because we have 4 columns here. First convert the given matrix into row echelon form say u. We now look at an example of finding a basis for n a.

It follows that the nullspace of the matrix is given by. It is straightforward to see that this set is linearly independent and hence it is a basis for. Next circle the first non zero entries in each row.

Call the variable x 1 displaystyle x 1 as a basic variable if the first column has a circled entry and. The null space calculator will find a basis for the null space of a matrix for you and show all steps in the process along the way. Comments and suggestions encouraged at email protected.

So if this is the reduce row echelon form of a let s figure out its null space. Thus the vector form solution to is. And we already know that the null space of a is equal to the null space of the reduced row echelon form of a.

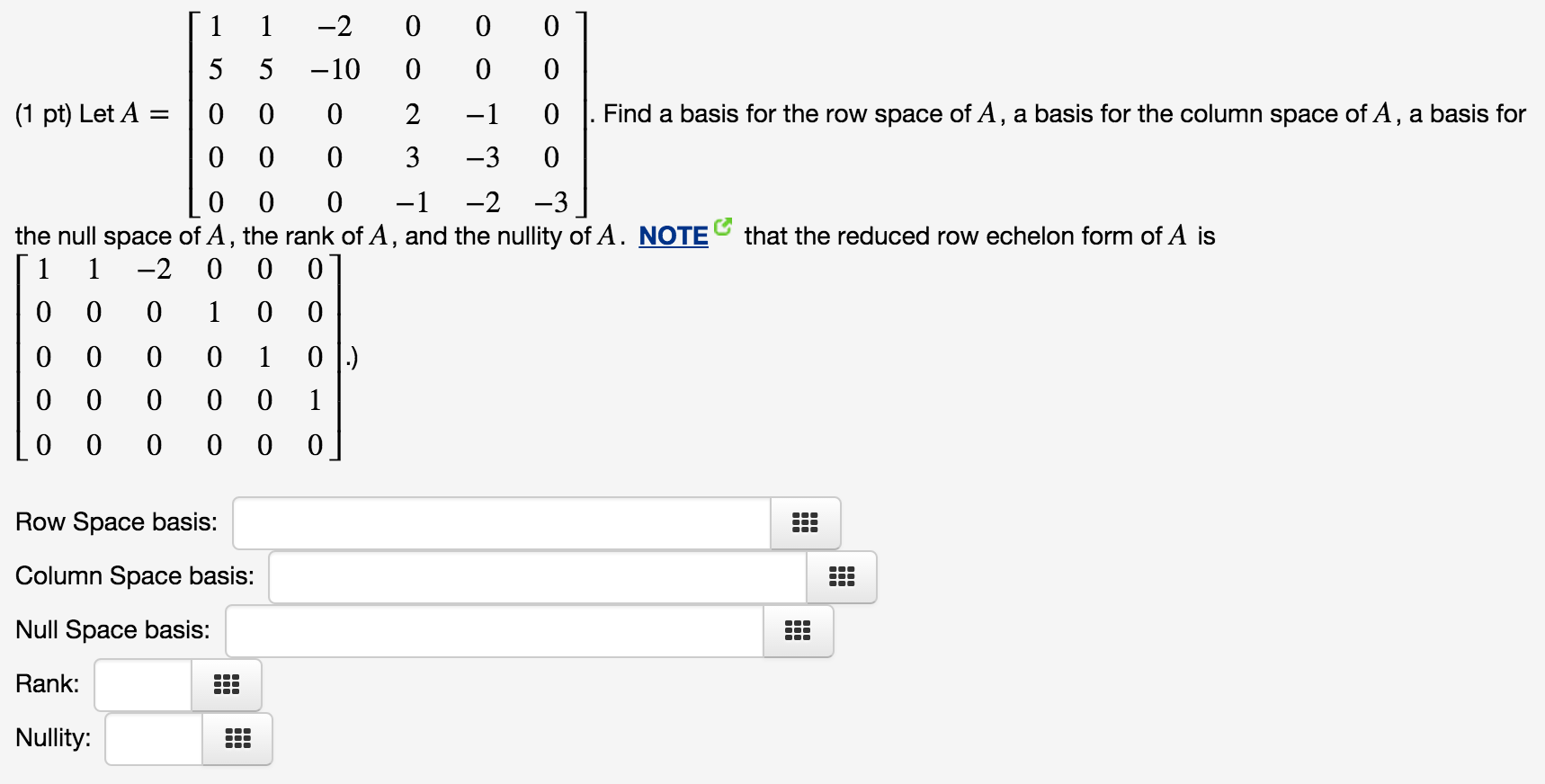
Hence the dimension of the nullspace of a called the nullity of a is given by the number of non pivot columns. Find a basis for the null space of the matrix a 1 0 3 2 1 0 2 2 4 4 0 0 0 2 6. A 1 1 2 2 2 4 2 3 5.

A find a matrix b in reduced row echelon form such that b is row equivalent to the matrix a. Let a r 2 4 be given by 1 1 1 3 2 2 0 4. 1 2 3 4.