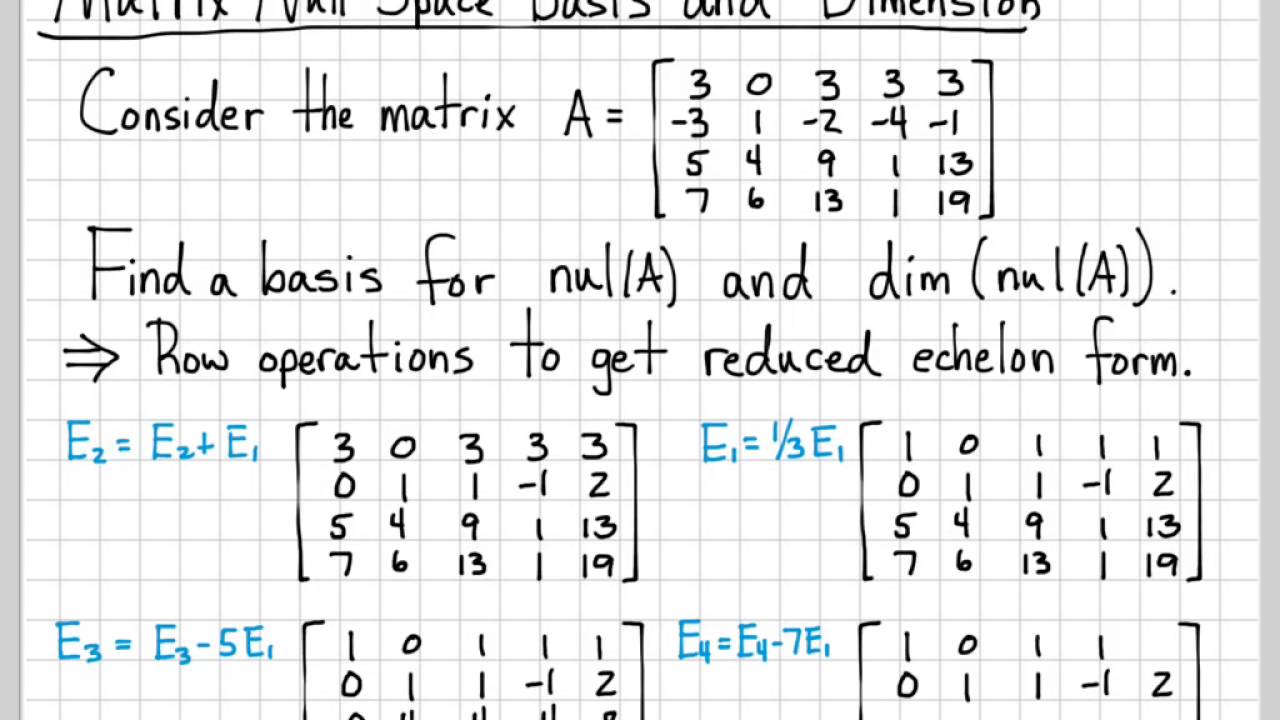Dimension Of Null Space

I have 1 2 3 vectors.

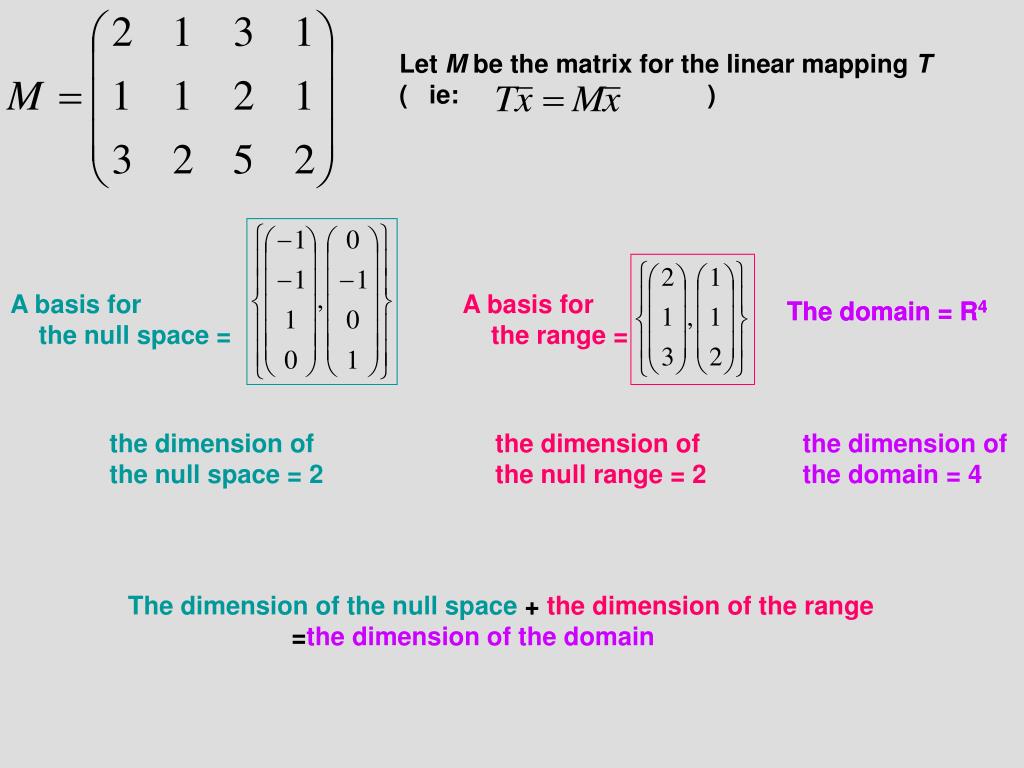
Dimension of null space. Nullity vs basis for null space there is a general method to nd a basis for the null space. The null space vectors b can be used to identify these linear relationship. So the dimension of the null space of b is 3.

Displaystyle operatorname rank a operatorname nullity a n where n is the number of columns of the matrix a. Well this is a basis set for b right there. The number of linear relations among the attributes is given by the size of the null space.

And that is also equal to 3. What is that the dimension of my null space of b. This null space is said to have dimension 3 for there are three basis vectors in this set and is a subset of for the number of entries in each vector.

The dimension of the row space of a is called the rank of a and the dimension of the kernel of a is called the nullity of a. The null space calculator will find a basis for the null space of a matrix for you and show all steps in the process along the way. These quantities are related by the rank nullity theorem.

This is illustrated in figure 1. The dimension of the null space is called the nullity of the matrix and is related to the rank by the following equation. Or another way to think about it or another name for the dimension of the null space of b is the nullity the nullity of b.

What will the picture look like if a is a 3 2 matrix and the null space is 0 dimen. The equation above is known as the rank nullity theorem. The nullity of a matrix a is the dimension of its null space.