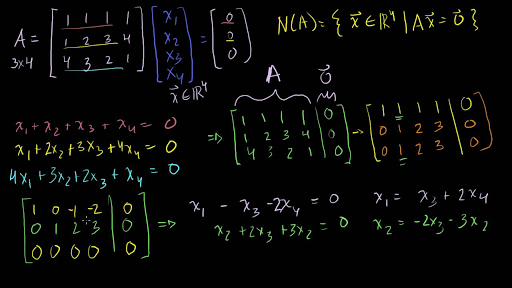Find The Null Space Of A Matrix

Comments and suggestions encouraged at email protected. The size of the null space of the matrix provides us with the number of linear relations among attributes. The null space of any matrix a consists of all the vectors b such that ab 0 and b is not zero.

first black astronaut in space final space trailer first man in space date first american to travel in space finger space fire from space final space season 1 episode 10 fire in space

Find The Null Space Of A Matrix Youtube

Linear Algebra Example Problems Null Space Example 2 Youtube

How To Find The Null Space Of A Matrix Example Youtube

Finding The Null Space Row Space And Column Space Of A Matrix Youtube

Find A Matrix Whose Null Space Is Equal To The Range Of The Matrix A Mathematics Stack Exchange

How To Find The Null Space Of A Matrix 5 Steps With Pictures

It can also be thought as the solution obtained from ab 0 where a is known matrix of size m x n and b is matrix to be found of size n x k.

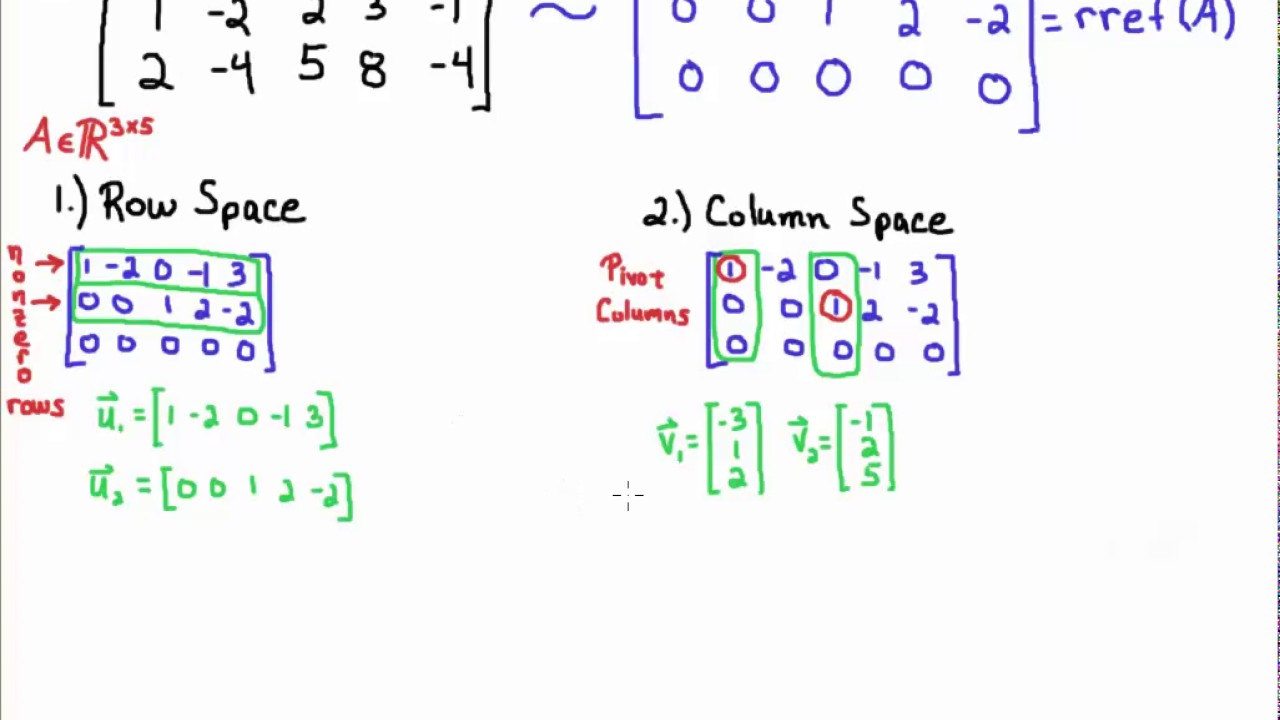
Find the null space of a matrix. That is if you let x 3 and x 4 be free variables the second equation directly above implies. Therefore the system is equivalent to. In general you can skip the multiplication sign so 5 x is equivalent to 5 x.

E 3x is e 3 x and e 3x is e 3 x. Rank a dim col a dim nul a displaystyle operatorname rank a operatorname dim operatorname col a operatorname dim operatorname nul a. The dimension of the null space comes up in the rank theorem which posits that the rank of a matrix is the difference between the dimension of the null space and the number of columns.

Also be careful when you write fractions. To determine this subspace the equation is solved by first row reducing the given matrix. In general you can skip parentheses but be very careful.

Since the coefficient matrix is 2 by 4 x must be a 4 vector. The calculator will find the null space of the given matrix with steps shown. Thus n 4.

1 x 2 ln x is 1 x 2 ln x and 1 x 2 ln x is 1 x 2 ln x. The nullspace of this matrix is a subspace of r 4. The null space calculator will find a basis for the null space of a matrix for you and show all steps in the process along the way.